Meteoroid fragmentation modeling
For most of the bright meteors (bolides or fireballs) recorded from multiple stations of the European fireball network (EN) we can calculate their atmospheric orbit and also their Solar System orbit. For the latter, it is crucial to know as accurately as possible the initial speed and the coordinates of the radiant of the meteor (the point in the sky from which it appears to originate). If these are very good observations, we can get a much more detailed description of the behavior of the original body (meteoroid) as it disintegrates in the atmosphere. In very rare cases, part of the meteoroid survives the passage through the atmosphere and meteorites hit the ground. We can then also determine the strewn field with an accuracy of hundreds of meters, allowing people to search for them efficiently. If found, the pedigree meteorites, as we call them, are an extremely valuable material for the study of the formation and evolution of the Solar System.
We use computer modeling to also derive some of the physical properties of meteoroids. This is based on very accurate data from the EN stations and the subsequently calculated atmospheric orbit of the body. What can we derive using modeling? In the case of smaller meteoroids and therefore weaker video meteors (millimeter-sized bodies), we can derive the bulk density of the material, how quickly it loses mass (ablation and erosion coefficients) and the masses of the constituent grains. For larger meteoroids (centimeter and decimeter bodies), which we observe as bolides, we have more and significantly richer data. We can therefore usually describe in more detail the destruction of such a body in the atmosphere, how quickly it loses mass, how many fragments it breaks up into at different heights above the ground, what are the masses of the grains it is composed of, and what is the mechanical strength of the meteoroid parts.
Data on bolides
What data do we have about the bolides? First of all, it is the radiometric curve (Figure 1), which describes the total bolide brightness at a very high temporal resolution (0.2 ms). This allows us to observe very sudden and short (hundredths of a second) flares of up to a few magnitudes (usually the result of the original body breaking into several pieces and releasing small dust grains), very rapid semi-regular brightness changes (so-called flickering), or gradual and long-lasting (tenths of a second) brightness changes.
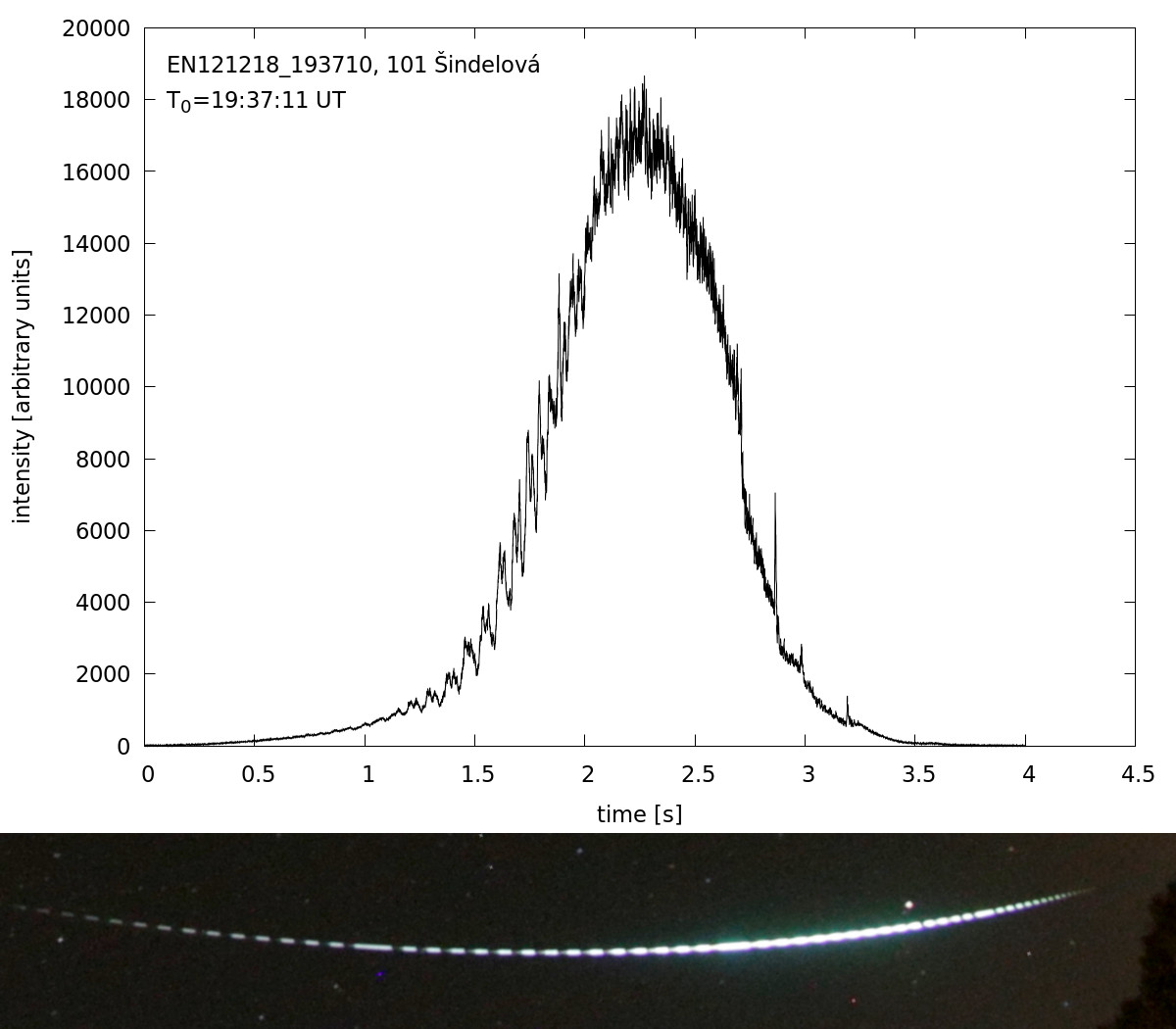
Figure 1. Radiometric curve of the Geminid EN121218_193710 taken by the DAFO camera at the Šindelová station with a temporal resolution of 0.2 ms. A crop from the digital all-sky image of this bolide is also included for comparison.
We have calibrated brightness information for the entire bolide from the all-sky images. For much of the flight of the longer fireballs, videos from the IP cameras and the fast-tracking video camera (called FIPS, Fireball Intelligent Positioning System) provide detailed images of the meteoroid breaking into individual pieces (Figure 2) and their subsequent motion. The all-sky image allows very important data to be derived on the velocity and deceleration of the fireball front (usually the foremost piece of the original meteoroid) throughout its orbit in the atmosphere, providing additional observational constraints on the physical model.

Figure 2. Video frames from a detailed video of the bolide EN300618_013421 taken by the FIPS fast-tracking system at the Kunžak Observatory. This record is used for a more detailed investigation of meteoroid fragmentation.
Physical model
In the modeling we use a physical model that describes the passage and disintegration of a body in the atmosphere. It contains the classical equations describing the meteoroid’s mass loss (ablation), its deceleration and the amount of light emitted, as well as fragmentation, i.e. the breaking of the meteoroid into smaller parts due to mechanical stress. The latter is present in virtually all observed meteors and must be included in the calculations.
Fragmentation in our model takes several forms. Often it is a sudden breakup, where the meteoroid is broken into several pieces, and usually also the release of dust, whose rapid ablation causes a sharp brightening of the bolide. However, we also observe gradual and longer lasting changes in brightness, which are probably caused by the gradual release of dust or larger particles from some part of the meteoroid. This process is called erosion.
Searching for a solution
To derive physical properties for a particular meteoroid, we need to find a match between the observed data and the physical model. We do this by appropriately choosing the free parameters of the model. From the radiometric curve, we can determine the times when the meteoroid broke into smaller fragments. Our task is to determine the number of fragments, their masses, the possible presence of eroding fragments or the amount and properties of the released dust grains. The traditional way is trial-and-error, where we choose these values randomly and based on long-term experience, and get a better and better agreement with observations (total bolide brightness, deceleration).
However, in recent years, we have also been developing a semi-automatic method that relies on genetic algorithms. The idea of using simplified rules for the evolution of life in programming dates back to the 1950s, but these algorithms developed more in the 1960s and 1970s and then en masse in the 1990s. Their strength lies in their versatility (they solve optimization problems in different domains) and robustness (they often find good solutions).
Figure 3 shows the radiometric curve of a bright Geminid (EN131218_012640) together with the model found by the genetic algorithm. Figure 4 then shows the deceleration for this Geminid. In both cases, the fit of the physical model to the observed data is excellent, so that the properties of the meteoroid in the model very likely match those of the observed body.

Figure 3: The radiometric curve of the Geminid EN131218_012640 (grey points) along with the modelled total bolide brightness (magenta curve), as well as the brightnesses of the fragments (black curves) and the released dust (green curves). The vertical dashed lines mark the moments of fragmentation of the meteoroid and its parts. The relative time in seconds is on the horizontal axis, the absolute magnitude is on the vertical axis.
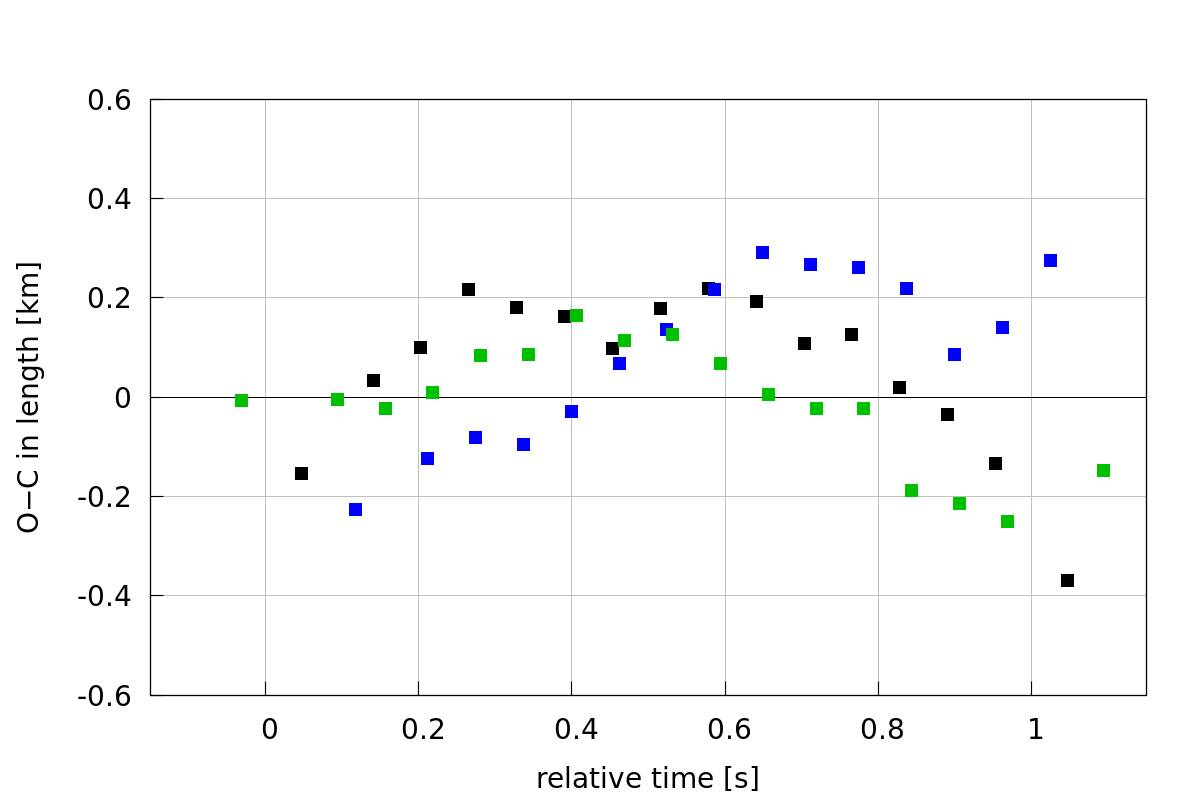
Figure 4: Residuals in the foremost fragment dynamics, i.e., the difference between the position from observations and from the model in kilometers (vertical axis) versus relative time in seconds (horizontal axis). The three colours correspond to the European fireball network stations.
What can we infer from the model?
We can now infer quite a lot of meteoroid properties from our model: its refined initial mass, the masses of the individual fragments released during fragmentation, the pressure acting on the fragment faces at the time of the breakups (and thus the mechanical strength of the fragments, which is proportional to the pressure), and the properties of the dust and larger grains released during the breakups. In rare cases, we can also calculate the final mass and velocity vector of fragments that survived the passage through the atmosphere (meteorites) and use a further procedure (dark flight calculation with the inclusion of a measured vertical wind profile) to determine the strewn field. Rarely a larger number of meteorites lands that are worth looking for. A number of such cases are listed on the exceptional fireballs page.
In this way, we are using cutting-edge data from the European fireball network to infer the physical properties of interplanetary matter. Recently, we have also been trying to use the faint meteor data from video observations for modeling, linking it to EN data for fainter bolides and describing the properties of meteoroids depending on size, from the largest (a few decimeters) to millimeter-sized bodies.